공머씨의 블로그
내가 공부한 논리회로 설계12.불대수를 이용한 최적화 본문
저번 포스팅에 이어서
이번 시간에도 계속해서 불대수를 공부할 것입니다.
17. 불 대수의 특성을 활용해서 논리 함수를 최적화하는 것을 공부합니다.

위와 같은 logic function이 있습니다.
아래와 같은 회로를 그릴 수 있습니다.

필요한 입력값들을 왼쪽에 그려놓고
게이트에서 필요로 하는 입력값들을 하나씩 끌어와서 그려주면 되겠습니다.
분기할 때는 항상 점을 찍어야 됩니다.
진리표도 아래와 같이 작성할 수 있습니다.
3개의 입력이 있으므로 8가지의 경우의 수가 있겠습니다.

여기서 생각해볼 것은 "Xnot Y Z는 언제 1이 될까? " 하는 것입니다.
X가 0이고(X not가 1) Y가 1이고 Z가 1일 때만 1이 됩니다.
AND게이트이기 때문에 입력 모두가 1일 때만 1이 출력됩니다.
tip:AND게이트에서는 출력이 1이 나오는 경우를 생각해서 출력 값을 작성
OR게이트에서는 출력이 0이 나오는 경우를 생각해서 출력 값을 작성
Xnot Y Znot는 언제 1일까? 를 생각해봅니다.
X=0, Y=1, Z=0일 때만 1이 됩니다.
입력에서 순서대로 010이라고 표기된 행에서의 출력은 1이 된다는 것을 알 수 있습니다.
비슷한 방법으로 XZ를 알아보겠습니다.
XZ는 X와 Z 모두 1일 때 출력이 1 이 됩니다.
왼쪽에서 해당하는 행을 찾아서 XZ가 있는 칸에 1을 작성해주고 나머지는 모두 0으로 채워주면 됩니다.
마지막으로 F를 결정하면,,,
3개 소자를 OR시켰음로 3개 중 하나라도 1이라면 1이 출력됩니다.
그 값을 찾아서 작성해주면 되겠습니다.
위 예시에서와 같이 수식을 곧이곧대로 회로를 그리는 것보다 최적화해서 변수와 항을 최소화시켜서 회로를 그려보도록 하겠습니다.
18-1. 최적화 과정

항의 개수와 변수가 최소화되어야 회로가 복잡하지 않게 그려진다는 것을 알 수 있습니다.
최적화에는 불대수를 이용한 방법과 카르노 맵을 이용한 방법이 있다고 했습니다.
먼저 지금까지 배운 불대수 항등식을 이용해서 최적화해보겠습니다

1항과 2항에서 공통인 항을 묶습니다.
이렇게 묶어놓으면 Z Znot이 OR로 연결되었으므로 1의 값을 갖는다는 것을 알 수 있습니다.
더 간단히 아래와 같이 나타낼 수 있습니다.

또 첫 번째와 두 번째 항을 보면 1과 어떤 게이트를 AND로 연결하면 두 개 모두 1이어야 1이 출력되므로
출력 값은 Xnot Y임을 알 수 있습니다. (이전에 배운 항등식을 외우고 있다면 그대로 적용해도 되겠습니다.)

위와 같은 식으로 간단하게 나타낼 수 있습니다.
이제 회로를 그려보겠습니다.

회로가 훨씬 더 간단해졌습니다.
18-2. 이제 진리표를 작성해보겠습니다.
0. 입력값이 뭐가 있는지 먼저 작성합니다.

1. Xnot Y를 먼저 알아보겠습니다.
둘이 AND로 연결되어있으므로 둘 다 1이어야 출력이 1을 갖습니다.
그래서 X가 0, (Xnot 이 1) Y가 1인 행을 찾습니다.
1로 채워줍니다.
나머지는 0으로 채우면 되겠습니다.

2. 그리고 XZ를 알아보겠습니다.
둘이 AND로 연결되어있으므로 둘 다 1이어야 출력이 1을 갖습니다.
X가 1일 때, Z가 1인 행을 찾으면 되겠습니다.
나머지는 0으로 채워주면 되겠습니다.

3. 최종적인 출력 F를 알아보겠습니다.

위와 같이 OR게이트로 연결되어있습니다.
둘 중 하나가 1이면 1이 출력되므로 F를 아래와 같이 작성할 수 있겠습니다.

아래와 같이 작성됩니다.

맨 처음 예시로 들었던 논리 함수의 진리표와 F를 비교해보면..... (00110101)

출력 값이 똑같은 것을 알 수 있습니다.
(항등식을 이용해서 풀었으므로 )
회로가 복잡해질수록 비용과 시간이 많이 듭니다.
아주 작은 딜레이라도 누적되면 엄청나게 많은 시간 차이가 나므로 최적화 과정은 중요합니다.
용어 정리
항: Term
변수: literal (Xnot, Y, Z 등등)
19. 추가로 몇 가지 Property를 알아보겠습니다.


EX1부터 알아보겠습니다.
첫 번째 항등식은 이전 포스트에서 설명했습니다.
19-2. 이 항등식을 바탕으로 두 번째 식을 풀어보겠습니다.

변수 X가 공통으로 있으므로 묶어줍니다.
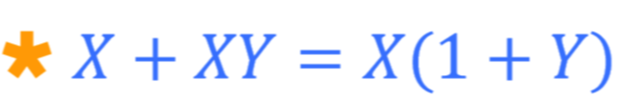
(1+Y)라는 식에서 1과 Y는 OR게이트로 연결되어 있으므로, 둘 중 하나라도 1이면 1이 출력됩니다.
따라서
X와 1이 AND게이트로 연결되어있는 논리 함수가 되고
AND게이트의 경우에는 둘 다 1이어야 1이 출력되므로 최종적인 답은 X가 됩니다.

X와 XY가 OR로 연결되었을 때 뒤에 있는 항인 XY가 떨어져 버리는 그런 형태가 됩니다.
이런 패턴을 기억해두면 유용할 것입니다.
19-3. EX1의 세 번째 항등식을 풀어보겠습니다.

이전 포스트 불대수의 항등식 15번에 있는 항등식을 이용하면 됩니다.

우변의 첫 번째 식을 보면 X와 /X가 OR로 연결되어있습니다.
둘 중 하나라도 1이면 1이 출력되므로 최종적인 값은 1입니다.
1과 (X+Y)가 AND게이트로 연결되어있는 형태가 남습니다.
AND게이트에서는 모두 1이어야 1이 출력되므로
1 또는 (X+Y)가 1이어야 합니다.
(X+Y)의 값에 따라 결정됩니다.
최종적인 결과는 X+Y가 됩니다.

EX1을 다음과 같이 정리할 수 있습니다.


첫 번째에 이미 공부한 항등식이 있습니다.
19-4. EX2의 두 번째 항등식을 풀어보겠습니다.
먼저 분배 법칙을 이용해서 다음과 같이 풀어줄 수 있습니다.

마지막항에서는 X와 (1+Y)가
1과 Y가 OR게이트로 연결되어있으므로 Y값에 상관없이 1이 출력 값이 됩니다.
이때 X와 1이 AND게이트로 연결되어있으므로 X값에 따라 X가 결정됩니다. (둘 다 1이어야 1이 출력된다.)
19-4. EX2의 세 번째 항등식을 풀어보겠습니다.
분배 법칙을 적용하여 전개하면 다음과 같아집니다.

X와 Xnot은 AND게이트로 연결되어있습니다.
둘 중 하나라도 0이면 0이 나오는 게이트인데 둘 중 하나는 무조건 0 이 될 수밖에 없으므로
0+XY가 항등식이 됩니다.
이런 경우에는 0과 XY가 OR게이트로 연결되어있으므로 둘 중 하나가 1이면 1이 출력됩니다.
따라서 XY로 출력 값이 결정됩니다.

19-5. 최종적인 출력 값들은 다음과 같습니다.

20. 쌍대성 (雙對性)
전기회로를 공부했다면 들어봤을 단어입니다.
사전적 의미는 아래와 같습니다.
두 회로 사이의 대응 관계의 유사성. 두 회로를 각각 따로 취급할 필요 없이 한쪽 회로의 해석 결과에 따라 대응 관계의 양을 바꾸어 주면 다른 쪽 회로의 해석 결과가 나온다.
(출처: 네이버 국어사전)
사전적 의미만 봐서는 와 닿지가 않으니, 아래의 설명들을 읽어보면서 이해하길 바랍니다.
20-1. duality
처음에 있는 3개 식과 아래에 있는 3개 식을 비교해보겠습니다.
서로 쌍대를 가지는 경우입니다.
첫 번째 식끼리 , 두 번째 식끼리, 세 번째 식끼리 dual입니다.

20-2. Duality Principle (쌍대 원리, 이중성 원리)
어떤 식이 있을 때 그 식의 Dual 식도 항상 성립한다는 원리가 있습니다.

추가로 괄호도 그대로 둡니다.
20-3. Dual 식을 만드는 방법에 대해 알아보겠습니다.

Variable(변수)는 그냥 그대로 두고,
AND는 OR로 각각 상호 교환하면 됩니다.
맨 위에 not기호를 붙여서 드 모르간 법칙을 이용해 풀어줄 때 위와 같은 원리를 적용시킵니다.
F의 출력 값을 알고 있는 상태에서 Fnot의 출력 값을 알고 싶다면
F의 출력 값에서 0과 1을 상호 교환하면 됩니다.
21.Consensus Theorem

유도하기 복잡하므로 확실히 암기해두는 것이 유리합니다.
한 줄씩 유도해보도록 하겠습니다.

(X+Xnot)는 1이므로 AND게이트 옆에 붙여서 써도 항등식이 됩니다.
두 번째 줄로 연결됩니다. (전개를 하면 됩니다.)

다음으로는 1번째 항과 세 번째 항을 , 두 번째 항과 네 번째 항을 이웃하게 작성합니다.
교환 법칙이 성립하므로 두 번째 식과 같은 식입니다.
공통된 식을 묶어주면 됩니다.

네 번째 줄과 같은 식이 됩니다.
괄호 안에 써져있는 두 개의 항을 살펴보면 1과 다른 입력이 OR로 연결되어있으므로 출력은 1이 됩니다.
여기서 각 항의 앞쪽에 있는 항과 1이 AND로 연결되어있으므로 앞쪽에 있는 항이 출력 값이 됩니다.
정리하면 다음과 같습니다.

이렇게 증명이 됩니다.
간간히 문제에 나오는데, 이런 결과를 냈을 때, 정리를 하고 규칙을 찾아서 숙지해두면 될 것 같다는 생각입니다.
22. 아래의 문제들을 풀어보길 바랍니다.

몇 가지 문제만 풀어보겠습니다.
나머지는 스스로 풀어보길 바랍니다.
1)


2)

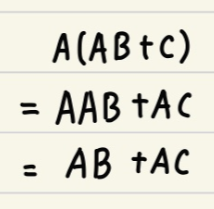
A(B+C)도 답이됩니다.
POS로 최적화한 경우입니다.(추후에 배웁니다.)
3)
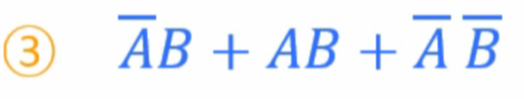


4)
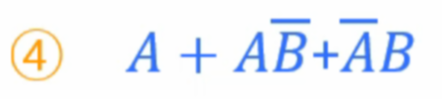

5)


A(B+C)
POS로 최적화한 경우입니다.(이후에 배웁니다.)
6)


A(/B+C)도 답이됩니다.
7)

8)

9)

10)

23. 마지막으로 Complement 에 대해서 공부해보겠습니다.
논리 함수에서 출력 값의 NOT을 물어볼 때가 있습니다.
이전에 공부했던 드모르간 법칙을 이용해서 풀면 됩니다.

다음과 같은 수식이 있습니다. /F를 구하시오

F not을 구하라고 했으므로 좌, 우변을 모두 NOT으로 만들어주면 됩니다.
두 번째 에서 세 번째 식으로 갈 때 드 모르간 법칙을 사용하면 됩니다.
위의 bar를 하나 없애고, OR를 AND로 바꾸어줍니다.

앞의 항과 뒤의 항에 드 모르간 법칙을 적용해주면 됩니다.
앞쪽 항부터 살펴보면 3개의 변수에 드 모르간 법칙을 사용하면
아래와 같은 원리가 사용됩니다.

또한 NOT이 짝수개 붙으면 사라진다는 원리도 적용해주면 되겠습니다.
뒤쪽의 항도 마찬가지입니다.

예제를 풀어보겠습니다.(F2의 NOT을 구하시오.)

NOT가 있을 때 드 모르간 법칙을 계속 반복합니다.

위와 같은 과정을 거칩니다.
예제를 더 풀어보겠습니다.
(F를 간단하게 하시오.-드 모르간 법칙을 활용해서 간단히 해야 하는 문제입니다. )


드 모르간 법칙을 확실히 알아두으면
1. 보수를 구하거나
2. NOT기호가 많이 포함되어있는 수식을 간단하게 해야 할 때
유용하게 사용할 수 있습니다.
NOT이 NOT을 만날 때, NOT이 OR를 만날 때, NOT이 AND를 만날때, NOT이 변수를 만날때
어떻게 달라지는지를 확실하게 알고 있어야 합니다.

24. 요약
지난 시간에 이어서 다음과 같은 내용을 공부해보았습니다.

1. 이진 논리와 이진 논리 게이트에 대해서 배웠고
2. 불대수의 기본적인 항등식 (17개 정도)
3. 항등식을 이용해서 최적화하는 방법 불대수의 기본적인 Property를 이용해서 회로를 간단히 해서 최적화하는 기법.
4. 게이트의 보수를 구하는 방법에 대해서 공부했습니다.
다음 시간에는 Maxterm과 minterm에 대해 공부해보겠습니다.
'내가 공부한 3학기 전공 > 내가 공부한 논리회로 설계' 카테고리의 다른 글
| 내가 공부한 논리회로설계14. Maxterm, POS(Product of Sum) (0) | 2020.05.03 |
|---|---|
| 내가 공부한 논리회로 설계13. Minterm과 SOP 최적화 (0) | 2020.04.30 |
| 내가 공부한 논리회로 11. 불대수(Boolean Algebra) (0) | 2020.04.24 |
| 내가 공부한 논리회로 설계 10. Combinational logic circuits (0) | 2020.04.16 |
| 내가 공부한 논리회로 설계 9.CODE (2) | 2020.04.16 |




