공머씨의 블로그
내가 공부한 논리회로설계14. Maxterm, POS(Product of Sum) 본문
이전 내용을 리뷰하고 Maxterm을 공부해보겠습니다.
Product term 곱으로 표현된 항
그 중 일부는 Minterm이 될 수 있는데 Minterm이 되려면 모든 변수가 한번씩은 포함되어 있어야 한다고 했습니다.
Sumterm중에서도 일부의 경우에 Maxterm이라고 할 수 있습니다 .
마찬가지로 모든 변수가 포함되어있어야 합니다.
진리표만 보고 수식을 유도하기 위해서 Minterm을 공부했던것 입니다.
이번시간에 POS에 대해 자세히 공부할 것 입니다.
30-2. 이에 앞서 '내공논 13 마지막 문제' 에 대해 풀이해보겠습니다.
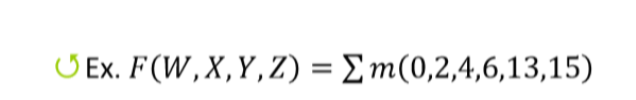
입력값이 4개 이므로 입력이 W,X,Y,Z인 진리표를 먼저 작성해보겠습니다.
Sum of Minterm을 이용할 때는 출력값이 1인 항에만 관심이 있으므로 출력값이 1인
m0 m2...m15의 F에 1이라고 작성해두고
이진수를 구한 다음, Minterm표현 규칙에 따라 변수를 작성하면 됩니다.
1) 아래와 같이 진리표를 작성할 수 있습니다.

2) 이를 그대로 Sum of Minterm으로 나타내면 다음과 같습니다.

3) 불대수 항등식을 이용해 최적화하면 다음과 같습니다.

4) 최적화된 논리함수를 이용해서 회로를 그려보면 아래와 같습니다

31. Maxterm의 개념에 대해 알아보겠습니다.

Maxterm에서는 출력값이 0일때 입력값에 관심을 갖습니다.
Minterm과 반대로 입력이 0이면 bar가 붙지 않습니다.
입력이 1이면 bar가 붙습니다.
각입력에 대해 위의 규칙을 가지고 Maxterm을 작성해보겠습니다.
아래 그림과 같이 완성됩니다.

Minterm과 마찬가지로 Maxterm의 순서에 따라 0~7까지 대문자M으로 맵핑시키면 다음과 같습니다.

M0를 채워보면 다음과 같습니다.
M0는 X+Y+Z 이고
0으로 채워진 부분은 0의 2진수가 X+Y+Z에 들어간 출력값입니다.

최종적으로 다음과 같이 작성될 수 있습니다.

32. Maxterm을 이용해서 진리표를 보고 회로를 그려보겠습니다.

위와 같은 진리표가 있습니다.
1)Product of Maxterm을 구하고
2) POS로 최적화한뒤(Product of sumterms)
3)회로를 구현하시오
회로를 어떻게 만들까?
지금까지는 Minterm을 이용하는 방법을 배웠었습니다.
방금 공부한 Maxterm을 이용해서 문제를 풀어보겠습니다.
Minterm과 반대로 f의 값이 0인 Maxterm들의 곱으로 표현하면 됩니다.
1) 출력값이 0인 값들을 찾아 아래와 같은 수식으로 작성할 수 있습니다.

그리스어 π의 대문자 입니다.
출력이 0인 입력에 관심.
2) 각 M0 M1 M4 M6에 대응되는 출력 게이트들을 작성해주면 됩니다.
여기까지 작성하면 Product of Maxterm을 구한것이 됩니다.

샛길: 진리표의 의미 살펴보기
수식에서F는 언제0일까요
F=ABCD의 꼴이니까 (항들의 곱)
F는 네가지의 Term 중하나라도 0이라면 0이 됩니다.
각 Term에서 언제 출력이 0이되는지를 알아보겠습니다.
첫번째 항이 0이 되려면 X=0,Y=0,Z=0이어야 됩니다. (항안에서는 변수들의 OR게이트로 연결되어 있으므로)
두번째 Term이 0이 되려면 X=0,Y=0,Z=1 이라면 0이됩니다. 그외의 경우에는 두번째 Term이 0이 될수 없습니다.
세번째 Term이 0이 되려면 X=1,Y=0,Z=0 이라면 0이 됩니다.
네번째 Term이 0이 되려면 X=0,Y=0,Z=1 이라면 0이 됩니다.
지금 우리의 관심은 F는 언제 0인지를 생각해보는것 입니다.
수식의 의미였습니다.
그 의미를 표로 나타낸것의 진리표입니다.
그러니까 각 입력에 대해서 Maxterm을 정리하면
출력 F는 값이 0인 Maxterm들의 곱으로 표현된다.
진리표와 수식이 완전히 같은 의미입니다.
진리표가 있을때 Minterm의 Sum으로도 Maxterm의 Product로도 표현할 수 있습니다.
다시 본론으로 돌아와서
F에 대한 수식을 적었는데 이 수식에 대해서 조금 더 간단히 할 수 있겠습니다.
힌트 (A+B)(A+C)=A+BC
3) POS로 최적화하라고 한다면
SumTerm의 곱형태이면서 제일 간단한 다음과 같은 항이 답이 됩니다.
Product of sum!

두번째 줄에서 빨간색 밑줄로 공통인 변수를 표시했습니다.
파란색글씨로 써진 공식을 이용해서 세번째 줄과 같이 최적화하고
최종적인 논리함수가 네번째 줄과 같이 나오게됩니다.
Product of Maxterm : 합들이 곱으로 표현하라고 하였으므로 더이상 최적화 하면 안됩니다.
4) 회로를 그려보겠습니다.

∴지난 번에 공부했던 Minterm하고 반대의 형태를 띄게 됩니다.
33. 예제를 한 번 풀어보겠습니다.
다음 진리표를 보고 MaxTerm을 이용해서 최적화 하는 문제입니다.

1) Product of Maxterm을 구해보고
E라고 하는 출력값에서 0인것을 먼저 찾습니다 .
E(X,Y,Z)=ΠM(3,6,7)
E=M3∙M6∙M7과 같이 표현하기도 합니다.
E= (X+/Y+/Z)∙(/X+/Y+Z)∙(/X+/Y+/Z)
위와같이 작성하면 됩니다 .
2) POS로 최적화한뒤
E= (X+/Y+/Z)∙(/X+/Y+Z)∙(/X+/Y+/Z)
이식을 풀어서 적으면 다음과 같습니다. 마지막항을 복제합니다.


3)회로를 구현하라.
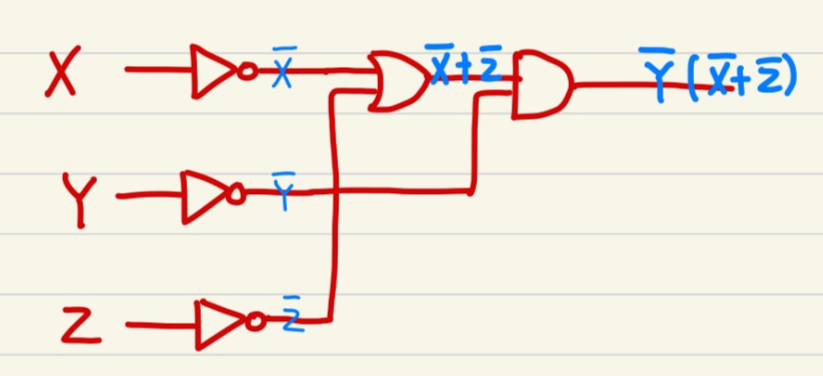
34. Minterm과 Maxterm의 관계에 대해서 알아보겠습니다.
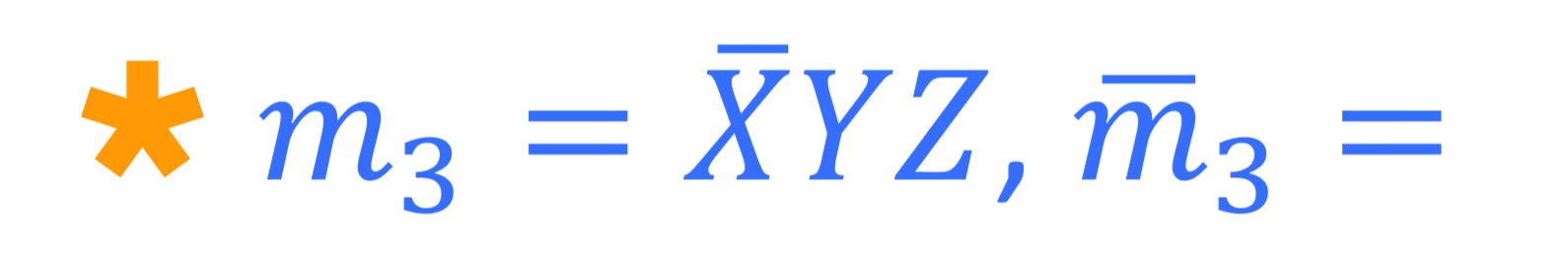
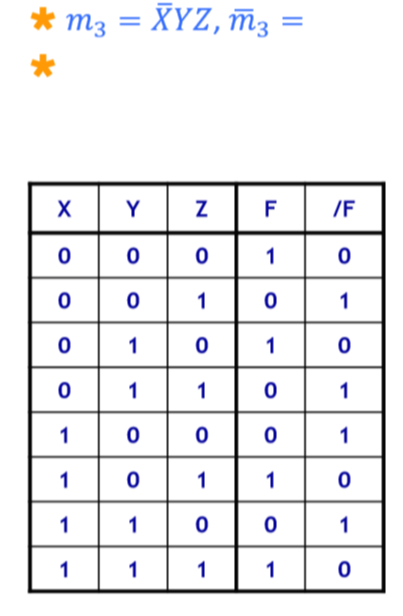
아래의 진리표에서 m3를 구해보면 (011) /XYZ입니다.
m3에 bar를 씌운뒤, 드모르간 법칙을 사용해서 풀어주면 다음과 같은 과정을 거칩니다.
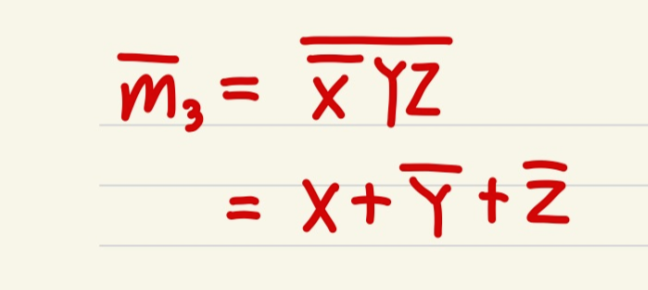
드모르간 법칙을 이용해서 바꾸어 주면 아래와 같이 Maxterm의 형태가 된것을 볼수 있습니다.

진리표로 대응시켜서 몇번째 Maxterm인지 보면 M3가 됩니다.
결론적으로 Minterm과 Maxterm의 관계를 수식으로 표현하면 다음과 같습니다.
/mi=Mi

(i번째 minterm의 NOT과 i번째 Maxterm이 같다는 의미입니다 .)
간단한 예시
다음과 같이 입력이 X Y Z 이고 F라는 출력을 가진 진리표가 있습니다.

출력값을 보고 Sum of Minterm 으로 작성하면

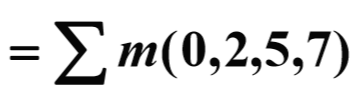


]
위와 같이작성할 수 있습니다 .
그리고 진리표에서 F의 NOT을 생각해봅니다.

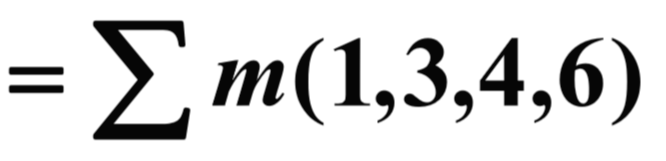

F NOT을 Minterm으로 작성하면 다음과 같습니다.

F NOT을 표현한 위 식의 bar를 붙여서 다음과 같이 표현해보겠습니다.
( bar을 붙였으므로 다시 F가 됩니다.)


그리고 드모르간 법칙을 이용해서 풀어주면 위와 같습니다 .
Minterm 1의 NOT는 Maxterm1과 같습니다. (위에서 설명함.)
다음과 같이 Maxterm으로 표현할 수 있습니다.


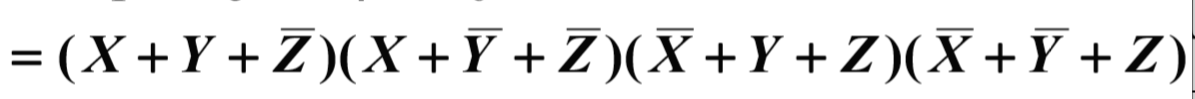
Minterm의 Sum이나 Maxterm의 Product로 표현할 수 있는데
Minterm의 Sum은 F의 값이 1인 입력들의 합으로 표현,Maxterm의 곱으로 표현하려면 F값이 0인 입력들의 곱으로 표현
된다는 것입니다.
다음과 같이 정리할 수 있습니다.

35. Minterm,Maxterm 요약

출력F값이 모두 1인 진리표가 있다고 가정하면
모든 Minterm을 최적화하면 F=1이 나오게 됩니다.
Maxterm도 이와 마찬가지 입니다.
'내가 공부한 3학기 전공 > 내가 공부한 논리회로 설계' 카테고리의 다른 글
| 내가 공부한 논리회로 설계16.K-map (3 inputs) (0) | 2020.05.08 |
|---|---|
| 내가 공부한 논리회로 설계15. K-map (2 inputs) (4) | 2020.05.06 |
| 내가 공부한 논리회로 설계13. Minterm과 SOP 최적화 (0) | 2020.04.30 |
| 내가 공부한 논리회로 설계12.불대수를 이용한 최적화 (0) | 2020.04.26 |
| 내가 공부한 논리회로 11. 불대수(Boolean Algebra) (0) | 2020.04.24 |




