공머씨의 블로그
내가 공부한 논리회로 11. 불대수(Boolean Algebra) 본문
지난 시간에 이진 논리와 이진 논리 게이트에 대해 공부해보았습니다.
간단하게 리뷰해보겠습니다.
이진 논리라고 하는 것은 0과 1로 판별하는 논리를 말합니다.
Binary logic gate는 Binary logic을 다루는 소자를 말합니다.
저번 시간에 배운 Gate들은 다음 그림과 같이 여러 가지 전자회로의 구성품인 전자소자라고 공부했습니다.
기초과목에서는 전자회로 내부에 신경 쓰지 않고 전자소자의 입력과 출력에 대해서만 다룹니다.

조금 넘어가서 진리표,타이밍 다이어 그램에 대해서 배웠고 게이트 3개에 대해 자세히 공부했습니다.
여기에 이어서 불대수라는 것을 공부해보겠습니다.

선형대수 이런 교과목들을 배웠을 거고
대수학 하면 어려울것 같지만 0과 1을 다루는 대수이기 때문에 불대수는 어렵지 않습니다.
2.2단원의 키워드는 불대수입니다.
-
도입
-
기본 개념
-
대수 조작과
-
함수의 보수
이번 포스팅에서는 2번 기본개념까지 공부할 것입니다.
10. 불대수는 영어로 Boolean Algebra라고 합니다.
Boolean에는 다음과 같은 뜻이 있습니다.
"불 방식의" (특히 컴퓨터와 전자공학에서 참과 거짓을 나타내는 숫자 1과 0만을 이용하는 방식)
어느 분야를 공부하든 간에 용어 정리를 잘해두어야 합니다.
11. 논리함수를 보고 회로로 구현하기

위와 같은 하나의 논리 함수가 있습니다.
논리 함수가 있을 때 이 논리 함수와 동일한 기능을 수행하는 회로를 그려보세요.
수식을 보는순간
-
"출력은 F이구나"
-
"입력은 X, Y 두 가지이다."
라고 생각해야 합니다.
회로도를 다음과 같은 단계들을 거쳐서 그릴 수 있을 것입니다.
1.X와 Y가 입력입니다.

2. X NOT이므로 다음과 같이 그려줍니다.

3. 또 중간에 +기호로 연결되어 있으므로 중간에 분기를 해서
다음과 같이 AND게이트를 그립니다.

분기를 할 때는 점을 찍어주어야 합니다.
4.XNOT회로 만들고 XY회로 만들고 그 두 개를 OR 시킨 것.
아래와 같이 그려집니다.

논리 함수가 있을 때 회로를 쉽게 구할 수 있습니다.
하나씩 그대로 그려주면 됩니다.
12. 반대로 회로가 그려져 있을 때 논리 함수를 작성할 수도 있어야 합니다.
아래와 같은 방법으로 Gate위에 어떤 식인지를 작성해보면서 아는 방법이 있습니다.

"logic Function=회로"라고 생각하면 됩니다.
그다음 진리표를 살펴보겠습니다.

위와 같은 진리표를 채워보겠습니다.
1. 먼저 진리표에 x와 y를 적습니다.
입력의 경우의 수를 생각해서 채워봅니다.

2. F를 바로 알 수 없으므로 항을 하나씩 나눠서 계산합니다.

입력 모두 1인 부분에서 출력이 1이 됩니다.
3. 그 두 개가 OR니까 F를 계산할 수 있겠습니다.

진리표를 보고 수식이나 그림을 알고 싶다면 다음 시간에 Minterm이나 Maxterm 공부하면
진리표를 보고 잘 조합해서 logicg Function이나 회로도를 알 수 있습니다.
Xnot과 XandY 둘 중 하나라도 1인 곳에서 F가 1 이 됩니다.
EX. 또 다른 문제를 해결해봅시다.
아래와 같은 회로도가 있습니다.

입출력 관계식을 적으라고 한다면 아래와 같은 같이 왼쪽에 있는 소자들이 출력 값부터 하나씩 작성한 뒤, 연결해주면 됩니다.

아래와 같은 수식이 나오게 됩니다.

진리표를 작성해보겠습니다
1. 일단 입력값을 아래와 같이 쭉~적어줍니다.
X의 경우 그대로 작성해주면 됩니다.

2. Ynot Z는 특정한 경우에만 값이 1이 됩니다.(AND Gate는 입력이 모두 1일 때만 1이 나온다. )
그게 어떤 경우인지를 조금만 생각해보면
Y가 0이고 Z가 1일 때 1이나 옵니다.
Ynot이 1이 되고 Z가 1이기 때문입니다.

3. 두 개를 OR 해서 마지막으로 F를 계산해서 구하면 됩니다.
(OR>> 1이 하나라도 있으면 1이 나온다. )

함수를 알고 있으면 회로 작성과 진리표 작성이 가능하다는 것을 공부해보았습니다.
진리표 작성에서 회로도 작성은 다음 시간에 공부합니다.
13. 불대수에 대한 간단한 개요
입출력이 다음과 같이 주어져 있다.

경우에 따라서는 최적화된 경우가 아닐 수도 있다.
곧이곧대로 회로를 작성한다면 복잡해집니다. 수식을 변형하여 동일한 기능을 수행하면서도 더 간단한 모양의 회로를 만드는 것이 필요합니다.
그것을 Optimization (최적화)이라고 합니다.
회로를 간단하게 만드는 데에 두 가지 방법이 있는데
1. 불대수를 이용하는 것과
2. 카르노 맵을 이용하는 방법이 있습니다.
두 가지 모두 잘 알아두어야 합니다.
2학기 때는 대부분 k-MAP을 사용하여 문제를 풉니다.
1학기 때는 불대수를 이용해서 푸는 방법도 잘 알아두어야 합니다.
14. 불대수가 뭔지 공부해보겠습니다.
Boolean에는 다음과 같은 뜻 이 있습니다. 불 방식의(특히 컴퓨터와 전자공학에서 참과 거짓을 나타내는 숫자 1과 0만을 이용하는 방식)
불대수라고 하는 것은 기본적으로 이진 논리에 관한 대 수합입니다.
두 가지 기능을 가지고 동작하는 경우에 여러 가지 protocol을 따지는 것이 불대수입니다.
아래와 같이 두 개의 표가 있습니다.
왼쪽은 OR Gate이고 오른쪽은 AND Gate입니다.

AND OR NOT에 대해서
항상 성립하는 Property를 이야기할 수 있겠습니다.
15. 몇 가지 항등식이 존재함을 이야기해보겠습니다.
아래와 같은 표를 채워보겠습니다.

[1] X+0
X라는 값은 0일 수도 있고 , 1일 수도 있습니다.
다음과 같은 회로를 이야기합니다.

OR게이트로 연결되어있으므로 둘 중 하나라도 1이면 1이 출력됩니다.
X에 1을 넣으면 출력은 1
X에 0을 넣으면 출력은 0
이라는 말이 됩니다.
그래서 "X값이 그냥 그대로 나오므로 출력은 X이다." 라고 할 수 있는 것입니다.
[2] X∙1=

AND게이트는 둘 다 1이어야 1이 출력되므로 X+1일 때 X값과 같은 값이 회로의 출력 값(F)이라고 할 수 있습니다.
[3] X+1=

OR Gate는 하나라도 1이면 출력 값이 1이므로
답은 1이 됩니다.
[4] X∙0=

AND Gate는 하나라도 0이면 출력이 0이므로 부등호 오른쪽은 0으로 고정된 값입니다.
[5] X+X=

잘 모르겠다 싶으면 0과 1을 대입해봅니다.
X가 0이라면 출력은 0(0과 0의 0R)
X가 1이라면 출력은 1(1과 1의 0R)
X값이 그대로 출력됨을 알 수 있습니다.
[6] X∙X=

마찬가지입니다.
[7] X+/X

둘 중 하나는 반드시 1 이 있기 때문에 1이라는 값이 출력 값이 됩니다.
(OR게이트는 둘 중 하나라도 1이면 1을 출력합니다. )
[8] X•/X

둘 중 하나는 무조건 0이 됩니다.
따라서 출력 값은 0이 나오게 됩니다.
(AND게이트는 입력값이 모두 1이어야 1이 출력됩니다.
반대로 생각해보면 하나라도 0이면 0이 출력됩니다.)
[9]

반전에 반전을 하니까 자기 자신이 나오게 됩니다.
추가로 XNOT이 짝수개 있으면 X위의 작대기가 짝수개 있으면 자기 자신이 나오고
X위의 작대기가 홀수개 있으면 반전 값이 나오게 됩니다.
약간 다르게 아래와 같이 그려볼 수도 있습니다.
(NOT게이트가 연속적으로 두 개로 연결)

[10]
일반적인 대수 계산에서와 같이 교환 법칙이 불대수에서도 적용됩니다.
[11]
일반적인 대수 계산에서와 같이 교환 법칙이 불대수에서도 적용됩니다.
[12]
괄호를 다른 항으로 묶어주어도 등식에 변함이 없습니다.
[13]
[12], [13] 같은 경우에는 결합 법칙이 성립한다는 이야기입니다.
[16] [17] 먼저 해보겠습니다.
[16]
[17]
드 모르간 법칙이라고 하는 것입니다.
X와 Y의 OR의 NOT는 각각에 NOT이 붙은 것 과 같아집니다.
XANDY에 NOT가 붙으면 각각에 NOT이 붙은 것 에 OR가 붙게 됩니다.
위와 같은 성질을 발견한 사람이 드 모르간이라고 합니다.
쉽게 증명할 수 있는데 증명은 생략하도록 하겠습니다.
[14], [15]
분배 법칙이라는 것입니다.
[14]의 경우에는 일반적인 수식에서 분배하는 것과 같습니다.
불대수에만 성립하는 독특한 법칙이 하나 있습니다.
일반적인 대수학에서는 볼 수 없는 모양입니다.
아래와 같이 생긴 수식을 분배합니다.

다음과 같은 과정을 거칩니다.

이 부분 때문에 많이 틀리기 쉽습니다.
잘 활용할 수 있을 정도로 익숙해져야 할 것 같습니다.
이게 왜 성립하는가?? 궁금하다면,
진리표를 작성해보시면 됩니다.


불대수의 Property를 입력할 때 진리표를 활용해서 같다고 입증해주면 됩니다.
여기까지 불대수의 기초적인 항등식까지 공부해보았습니다.
16. 몇 가지 더 comments 해보면
16-1. 두 번째 줄의 출력 값은?

왜냐하면 n input OR Gate에서 입력하나가 1로 고정이 되어 있으면
다른항이 무엇이든지 출력은 무조건 1이 됩니다.
(OR게이트에서는 입력이 몇 개든 상관없이 입력 중 하나라도 1이면 1이 출력됩니다.)
위 두 문제의 답은 둘 다 1이 됩니다.
16-2. 다음 식을 불대수 항등식을 이용해 간단하게 만드시오.

불대수에서만 성립하는 항등식 입니다.


[15] 번의 경우에는 불대수에서만 성립하는 독특한 분배 법칙입니다.
A OR BCD라고 답하면 됩니다.
아래와 같이 작성해주어도 답이 됩니다.
(A+B)(A+C)(A+D)
OR가 있든 AND가 있든 분배 법칙은 항상 사용할 수 있습니다.
많은 연습이 필요한 부분입니다.
16-3. 다음은 드 모르간의 일반식에 대한 이야기입니다.

위에서는 2 Input에 대해서만 설명했는데 두 개의 입력뿐만 아니라 일반적인 경우에도 성립을 한다는 것입니다.
OR는 AND로
AND는 OR로 바뀐다.
NOT은 쪼개진다.
16-4. 이제 몇 가지 연습을 해보겠습니다.

1)

AND Gate에서 입력하나 가 1이면 다음과 같다고 할 수 있습니다.

답은 A+B+C가 됩니다.
2)

OR Gate는 입력하나 가 1이면 나머지 3개에 관계없이 출력은 항상 1이 됩니다.
답은 1이 됩니다.

3)

하나라도 1이 있으면 1이 출력되므로 출력은 1이 됩니다.
AND로 연결된 ABC의 값에 상관없이 답은 1이 됩니다.
4)

A가 0일 때와 A가 1일 때의 경우를 나누어 생각해봅니다.
1. A가 0인 경우 /A은 1입니다.
첫 번째 항은 AND게이트로 연결되어있으므로 둘 다 1이어야 1이 출력됩니다 첫 번째 항은 1입니다.
두 번째 항 A는 가정한 대로 0입니다.
첫 번째, 두 번째 항이 OR게이트로 연결되어있으므로 둘 중 하나라도 1이면 1이 출력됩니다.
최종적인 답은 1입니다.
2. A가 1인 경우 /A은 0입니다.
첫 번째 항은 AND게이트로 연결되어있으므로 둘다 1이어야 1이 출력됩니다 첫번째 항은 0입니다.
두 번째 항 A는 가정한 대로 1입니다.
첫 번째, 두 번째 항이 OR게이트로 연결되어있으므로 둘 중 하나라도 1이면 1이 출력됩니다.
최종적인 답은 1입니다.
익숙해지면 이렇게 길게 생각하지않고도 답이 나오니 복잡해보인다고 걱정하지않아도 됩니다.
A가 0이든, 1이든 최종적인 답은 1입니다.
5)

ANOT과 A는 두 개를 AND 시켰으므로 0이 됩니다
0과 AND로 연결된 회로는 일단 0 이 됩니다.
오른쪽의 ENOT과 E 또한 마찬가지로 0 이 됩니다.


0과 다른 Gate를 OR 시키면 남는 Gate에 따라 출력 값이 결정되므로
아래와 같은 등가 Gate를 구할 수 있습니다.

DNOT과 D 둘 중 하나는 0이 됩니다.
AND Gate는 두 개 모두 1이 되어야 1을 출력하므로 (하나라도 0이면 0을 출력하므로)
최종적인 출력 값은 0 이 됩니다.
6)


7)


8)
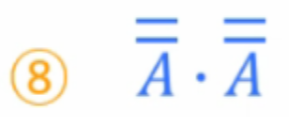

9)

순서가 바뀌어도 AND나 OR는 교환 법칙이 성립한다.라고 공부했습니다.
첫번째 항은 전체가 0이 될 것입니다. (AND Gate는 하나라도 0이라면 0이 나오기 때문에 )
두 번째 항도 마찬가지입니다. OR Gate에서는 하나라도 1이면 1이나 오기 때문에 0을 무시하고 다시 아래와 같이 작성해줍니다.

위의 식을 분배 법칙을 이용해서 풀어줍니다.
결국 아래와 같은 식이 됩니다.

뒤에 있는 (1+D)라는 항이 어차피 1이 되므로
출력 값은 C의 입력과 똑같은 값으로 출력됩니다.
10)


기본적인 항등식을 공부해보았습니다.
처음 공부할 때 확실하게 공부해두어야 다음 과정으로 넘어가는 데에 무리가 없습니다.
문제를 꼭 스스로 풀어보고 답을 확인해보길 바랍니다.
'내가 공부한 3학기 전공 > 내가 공부한 논리회로 설계' 카테고리의 다른 글
| 내가 공부한 논리회로 설계13. Minterm과 SOP 최적화 (0) | 2020.04.30 |
|---|---|
| 내가 공부한 논리회로 설계12.불대수를 이용한 최적화 (0) | 2020.04.26 |
| 내가 공부한 논리회로 설계 10. Combinational logic circuits (0) | 2020.04.16 |
| 내가 공부한 논리회로 설계 9.CODE (2) | 2020.04.16 |
| 내가 공부한 논리회로설계8. Complement Number2. (0) | 2020.04.12 |




