공머씨의 블로그
내가 공부한 논리회로 설계 9.CODE 본문
이번에는 코드에 대해서 공부해보겠습니다.

1. 먼저 코드의 기초개념, 코드란 무엇인가에 대해서 공부합니다.
2. 그 다음 코드의 종류와 사용방법을 자세히 알아봅니다.
- BCD
- Parity Check Code
- Gray Code
- Alphanumeric code(키보드에 글자를 치면 컴퓨터에 어떻게 저장되는가?)
1) ASCII
2) 한글코드
3) 유니코드
아스키코드는 C언어에서 자세히 공부하게되고,
3) 4)번은 이런게 있구나 정도만 알면 될것 같습니다.
20. 먼저 code의 정의 (Definition)에 대해 알아 보겠습니다.
어떤 원본 데이터를 새로운 데이터로 바꾸는 '형태', '결과물', '과정'을 코드라고 합니다.
조금 더 구체적으로 이야기하면 다음과 같은 종류가 있습니다.
class 데이터 변환을 위한 코드
소스코드: data compressinon
데이터를 압축하는 코드(Mp4파일- 많은 용량의 데이터를 압축하는 것도 코딩이라고 볼 수 있다.)
채널 코드: data protection
데이터의 용량을 늘리는 코드도 있습니다.
왜? 무선으로 정보를 전송을 할 때 정보 전송 중에 오류가 생기기 쉬워 오류를 수정하거나 인지 하기 위해서 원래의 데이터보다 많은 양의 데이터를 만들어서 전송하기도 합니다.
첨언하자면 Data compression 같은 코드는 4학년 때 영상신호처리에서 배우게 됩니다.
그리고 채널 코드 같은 경우에는 데이터의 신뢰성을 부가하기 위해 공부하는 이동통신 시간에서 깊게 알아볼 수 있습니다.
논리회로 과목에서는 아래와 같이 간단히 데이터를 변환하는 코드 정도만을 공부합니다.
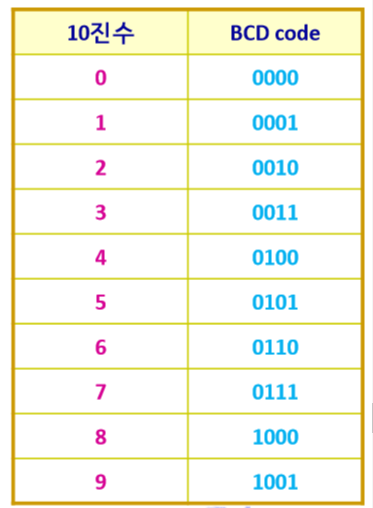
21. BCD Code (BCD Number)
BCD의 뜻은 2진수로 코드화 된 10진수라는 뜻이고 원리는 다음과 같습니다.
Binary-coded decimal
Principles: 4 bits로 0에서 9까지의 10진 정보를 표현합니다.
8421 코드라고도 합니다. (각 자릿값에 8421을 곱하기 때문에)
2의 3승, 2의 2승,2의 1승 ,2의 0승
아래의 table에 10진수와 BCD code가 있습니다.
인간은 10진수를 알지만 불행히도 기계는 0과 1만을 입력할 수 있습니다.
그래서 앞에서 between conservision을 공부했습니다.
십진수를 이진수로 바꿔서 정보를 처리하는 경우도 있지만
코드를 사용해서 맵핑하는 경우가 있습니다.
10진수 0에서 9까지 무조건 4bit로 할당하고 정의합니다.
4 를 0111이라고 정의하는 코드가 BCD코드입니다.
BCD코드 table는 딱 위의 표에 있는 10진수만 표현할 수 있습니다.
예를 들어 10진수 85를 BCD코드로 나타내려면
8,5를 각각 BCD코드로 바꾸는 것입니다.

그림과 같이 아래 첨자에 BCD를 작성해주어야 합니다.
EX. 십진수 15를 BCD코드로 바꾸면? (2진법을 사용해서 표현하라는 것이 아닙니다.)
1을 BCD 코드로 , 5를 BCD코드로 바꾼뒤 순서대로 연결합니다.
아래와 같게됩니다.

0~9까지 4Bit로 맵핑되었다는 사실만 알면 BCD테이블을 따로 외울 필요가 없습니다,
(아래 첨자에 2가 아닌 BCD를 표기하는 것에 주의해야 합니다.)
EX. 십진수 185를 BCD코드로 바꾸면?

BCD코드 하나가 4Bit로 구성되어 있으므로 자릿수가 n개 십진수를 BCD코드로 바꾸려면 4 ×n개의 bits가 필요함을 알 수 있습니다.
22-1. BCD코드로 덧셈하는 법을 공부해보겠습니다.
왼쪽은 십진수 덧셈입니다.
BCD코드로 바꾸어 덧셈을 하는 모습입니다.
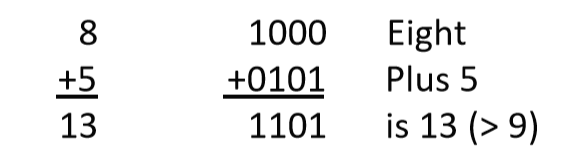
답을 아래와 같이 표현하면 틀립니다.

1101이라는 BCD코드는 없기 때문입니다.
BCD테이블에 있는 10개의 코드가 전부입니다.
각 BCD가 의미하는 게 하나의 십진수 숫자이기 때문입니다.
10이 되는 순간 하나가 올라가야 정답을 구할 수 있습니다.
(BCD코드는 0~9까지의 숫자가 맵핑된 코드이기 때문에)
실제 정답의 결과랑 현재 수행하는 결과를 보면 Carry가 6만큼의 오차가 있게 됩니다.
두 단계로 나누어서 계산을 해야 합니다.
첫 번째 단계는
이전에 배웠던 2진법의 덧셈을 수행하면 됩니다.
처음 수행했던 결과가 나옵니다.
두 번째 단계는 (필요한 경우에만 수행-덧셈의 결과가 10 이상인 경우)
다시 말해서 BCD결괏값을 십진수로 바꾸었을 때 9보다 작거나 같은 경우에는
답을 그대로 써주면 되는데
만약 9보다 크다면 ,,,
6을(BCD코드로 0110) 더해서 강제로 하나 올라가게끔 보정을 해주면 됩니다.
원래 10이 될 때 carry 가 생기는 덧셈을 해야 하는데
16일 때 carry 가 생기는 덧셈을 수행했기 때문입니다.
이것이 핵심입니다.
EX.
다시 해봅니다.

답을 작성할 때는 강제로 4bit 단위로 작성해야 합니다.
+다른 방법:8과 3을 더하면 십진수로 13입니다.
BCD코드로 13을 표현하면 BCD코드로 1, BCD코드로 3을 표현해주면 됩니다.
문제에서 풀이과정을 원할 수도 있으니 정석대로 하는 방법을 연습하길 바랍니다.
Q 십진수 18과 29를 BCD코드 형태로 덧셈을 하여라.
1) 먼저 18과 29를 BCD코드로 변환한 뒤

2) 2진수 덧셈을 해줍니다.

3) 10 이상인 수 이므로 마지막으로 십진수 6을 BCD코드 형태로 덧셈을 해줍니다.

또 다른 방법
십진수 상태에서 덧셈을 해서 나온 십진수 결과를 바로 BCD로 바꾸어 주는 방법도 있습니다.
어떤 방법으로 하든 답을 아래와 같이 표기해주면 됩니다. 아래첨자에 BCD라고 작성해야함을 주의 합니다.

22. Excess-3 code라는 코드도 있습니다

BCD코드에 3을 더한 코드를 Excess-3 code라고 합니다.
왜 이런 코드를 만들었는지?
BCD코드를 쭉 봤을 때 0의 개수가 1의 개수보다 많습니다.
Excess-3 코드는 0과 1의 개수의 균형을 맞추기 위해 등장한 코드라고 생각하면 되겠습니다.
BCD코드를 정확하게 이해하는 것이 더 중요합니다.
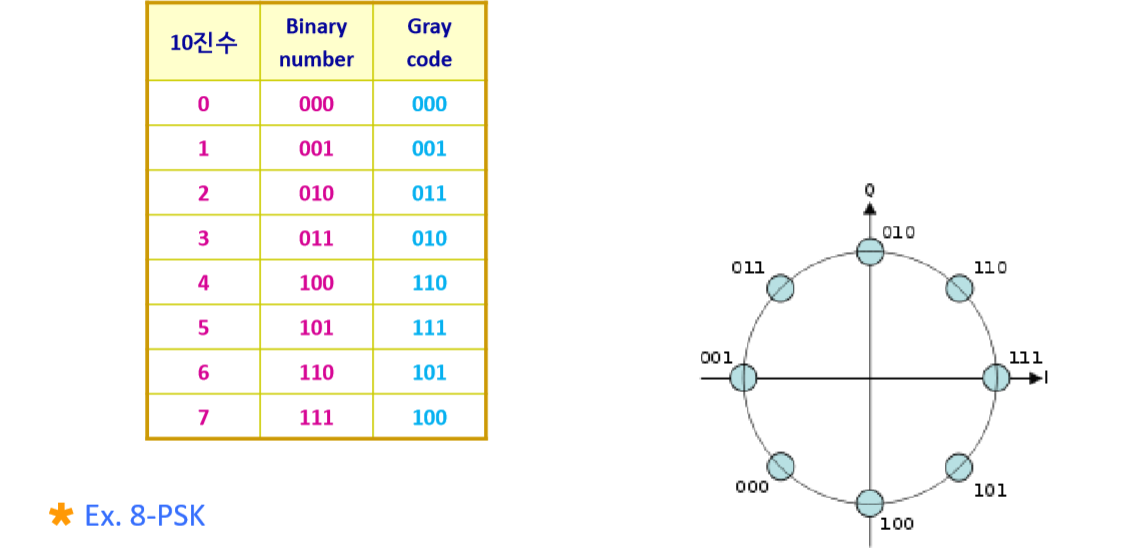
23 . Gray code라는 것이 있습니다.
원리는
디지털 통신에서 자세히 배웁니다..
변조방식 중에 8-psk라는 방식이 있습니다. 데이터를 보낼 때 신호처리를 하는데 위 그림과 같이 맵핑해서 보내는 것입니다.
그림을 잘 보면 데이터를 맵핑하는데.... (001에서 시작해서 시계방향으로 보면 되겠습니다.)
000이 있고 옆에 001 010이 와야 할 것 같은데 같은데 011이 있습니다.
이렇게 순서를 정해서 좋은 점은 인접한 바로 옆에 있는 심벌 간에는 오직 한 bit만 다르기 때문에 비트 오류가 줄어듭니다.
위 그림에서 보면 001에서 시계방향으로 첫 번째에 있는 011은 서로 두 번째 bit끼리만 다릅니다.
001에서 반시계 방향으로 있는 첫 2진수인 001도 마찬가지입니다.
항상 한 bit만 다르게끔 맵핑이 된다는 특징을 가집니다.
그런 식으로 bit를 나열한 코드를 Gray code라고 합니다.
나중에 통신에서 조금 더 자세히 공부합니다. 예를 들어 011을 전송했는데 전송 중에 에러가 발생해서
잘못 인지해도 1bit만 틀리게 되기 때문에 최대한 bit오류가 적게끔 하기 위한 기술입니다
24. Parity Check Code

통신 시스템에서 에러를 검출하기 위한 목적으로 만들어진 코드입니다.10001이라는 7BIT가 하나 있습니다.
앞 또는 뒤에 한 BIT를 추가합니다. 여기에 규칙이 있습니다.
Even parity의 경우에는 1의 개수가 짝수가 되도록 0 또는 1을 추가하면 됩니다.
이렇게 해서 만들어진 코드를 Even parity check code라고 합니다.
Odd Parity의 경우에는 1의 개수가 홀수가 되도록 Parity Bit를 추가합니다.
위치는 상관없고 0을 추가할지 1을 추가할지가 중요하다고 생각하면 됩니다.
EX. 예시를 통해 살펴보겠습니다.
만약 1010100에 1이 3개 있습니다.
앞에 1 또는 0중에 무엇을 추가해서 Parity Check Code를 만들지 생각해봅시다.
1의 개수가 짝수가 되게 하려면 1을 넣으면 됩니다.
위와 같이 1의 개수가 짝수가 되도록 bit한개를 추가하는 방법은 Even Parity라고 합니다.
이때 추가되는 Bit을 Parity bit라고 합니다.
EX.다음과 같은 5bit가 있습니다.
10110
"Even Parity Check code가 되도록 만들어라." 라고 한다면
110110이라고 하면 됩니다.
1의 개수가 짝수가 되도록 한bit추가한 코드는 Even Parity Check Code가 됩니다.
이러한 Parity Check Code는
전송 중에 오류가 발생했는지 아닌지 확인하기 위해 사용합니다.
자세한 예를 들면 원래 1000001을 보내고 싶었다고 합시다.
Even Parity 추가해서 0100001을 만들었습니다. 0100001을 transmit 했습니다.
receive가 받으면 RX 어딘가가 한 비트 깨져서 오류가 발생해서 0110001을 받았다고 생각해봅시다.
RX는 오류를 추적 하기 위해 먼저 1의 개수를 셉니다.
Tx가 오류를 보냈다고 error detection 할 수 있습니다.
Parity Check Code는 가장 기본적인 error detection 코드임을 알 수 있습니다.
나중에 통신 관련 교과목에서 자세히 공부하게 될 것입니다.
이런 방식에는 다음과 같은 한계가 있습니다.
Parity Check Code는 1bit 에러가 발생했을 때만 검출 가능합니다.
만약 2bit가 오류가 났다면 검출할 수가 없습니다.
오류가 났다는 것은 0이 1로 1이 0으로 바뀌었다는 것인데
2개가 오류가 나면 (1이 0으로 전송되고,0이 1이 전송된 경우)1의 개수에는 변함이 없기 때문이죠.
예를 들어 TX에서 01000001을 보냈는데
2bit 오류가 나면
10000001이 됩니다. 이럴 때 1의 개수는 2로 변함이 없어서 검출할 수 없습니다.
여러 비트를 검출하는 방법은 CRC코드라는 방법으로 검출합니다.
(Cyclic Redunancy Check) code
거의 모든 통신시스템에서 사용 코드입니다. 이에 대해서는 기초를 교과목을 먼저 공부한 뒤, 이동통신 교과목에서 공부합니다.
요약: Even Parity code와 Odd Parity code 를 만들 수 있으면 됩니다.
25. Alphanumeric Code라는 것이 있습니다.
Alpha라는 것은 '글자'라는 뜻입니다.
종류가 여러 가지 있는데 이 수업에서는 ASCII코드 만 잘 알고 있으면 됩니다.
25-1. ASCII CODE
사람이 키보드에 뭔가를 입력하면 컴퓨터가 무슨 글자가 들어왔는지 인식을 해야 합니다.
A=1000001
B=1000010
위와 같은 식으로 정의한 것입니다. 하나의 문자와 기호, 숫자를7bit로 표기합니다.
영어 알파벳, 숫자, 특수문자 등을 표현하려면 최소 7bit가 필요하기 때문에 입니다.
7Bit로는 총 128개의 경우의 수를 표현할 수 있습니다. (2의 7승=128)
영어 알파벳은 총 52개의 문자 (대문자 26, 소문자 26)
숫자는 총 10개 (0~9)
특수문자들 (!@$) 52개
최소 128가지 경우의 수가 필요하기 때문에 7bit로 나타낸 것입니다.
이는 "내가 공부한 c언어" 에 다음 포스팅을 참고하시기 바랍니다.(링크 첨부- 업데이트하자마자 바로 올리겠습니다.)
그래서 '7Bit로 알파벳과 숫자를 표기하기 위해 만든 표준'이 아스키코드입니다.
현재 대부분 컴퓨터 시스템의 입출력에 사용되는 코드입니다.

세로축 0~7까지는 3bit로 표기합니다. (000~111)
가로축의 0~F까지는 4bit로 표기합니다. (0000~1111)
세로축과 가로축을 읽어서 총 7bit로 읽을수 있습니다.
알파벳 A를 아스키코드로 표기하면 (세로축을 먼저 읽고-같은 행으로 가서 찾는다. 가로축을 읽으면 됩니다.-같은 열로 가서 찾는다.)
16진수로 41 입니다. (가로축에 F까지 있는것을 보면 16진수로 읽어야 함을 알 수 있습니다.)
이를 7bit로 구성된 이진수로 바꾸면 1000 001이 됩니다. (가로축은 4bit로 읽고 세로축은 3bit로 읽으면 됩니다. )
25-2. 8bit로 구성된 아스키코드도 있습니다.
확장 아스키코드(Extend ASCII Code)라고 합니다.
특수문자에 더 특수한 문자(128개)까지 표기할 수 있게 하기 위해 만들었습니다.
위 아스키코드 표에서 아래에 다음의 표를 그대로 붙였다고 생각하면 됩니다.

세로축을 3bit로 표현했었는데 1bit추가되어
0에서F까지 표현할 수 있게 되었습니다.(0000~1111)
25-3.EBCDIC라는 코드도 있습니다.

일반적인 범용 컴퓨터가 아닌 슈퍼컴퓨터나 IBM 컴퓨터에서 사용되는 코드입니다.
표현방법이 다릅니다.
아스키코드에서는 'a'를 1000001로 정의했습니다.
EBCDIC 코드에서는 'a'를 10000001로 정의되어있습니다.
이런 게 있구나 정도로만 알아두시면 됩니다.
25-4.한글코드
글자 하나하나를 16bit로 표현합니다. 두 가지 방법이 있습니다. 모두 대한민국 표준 코드입니다.
1. 조합형
초성 중성 종성에 각각 5bit로 표현합니다.
맨 왼쪽 자리에는 1이 붙습니다.

2. 완성형
한 글자가 이미 16bit로 완성되어있는 코드입니다.
박 바 밥
미리 define 되어있는 경우입니다.
(두 글자인 경우도 16bit인가?)
25-5.유니코드
한번 읽어보면 되겠습니다.

이렇게 해서 1단원을 마쳤습니다.

1.1
디지털은 무엇인가?
왜 사용하는가?
아날로그와 차이점은 무엇인가?
디지털 회로와 시스템에 대해 간략하게 알아보았다.
1.2
수체계, 진법
각각 상호 교환과 그 의미
1.3
각 진법에서 사칙연산을 공부 (Carry와 borrow의 규칙)
보수의 개념 (음수를 표현하기 위해 사용된다.)
1.4
Code (데이터를 필요에 따라 다른 형태로 변환하는 과정-코딩, 변환된 결과물- 코드)
다음 포스팅부터는 조합 회로와 불대수를 공부하겠습니다.
'내가 공부한 3학기 전공 > 내가 공부한 논리회로 설계' 카테고리의 다른 글
| 내가 공부한 논리회로 11. 불대수(Boolean Algebra) (0) | 2020.04.24 |
|---|---|
| 내가 공부한 논리회로 설계 10. Combinational logic circuits (0) | 2020.04.16 |
| 내가 공부한 논리회로설계8. Complement Number2. (0) | 2020.04.12 |
| 내가 공부한 논리회로 설계7-Operations(사칙연산 2),Complement Number (0) | 2020.04.12 |
| 내가 공부한 논리회로 6. Arithmetic Operations 1(사칙연산1) (0) | 2020.03.31 |




