공머씨의 블로그
내가 공부한 논리회로 설계18. PI, EPI 본문
지금까지는 카르노 맵을 공부 했습니다.
카르노 맵에 대해 총정리하자면,
입력 변수가 2~4개일 때, 출력을 입력의 함수로 최적화하는 쉬운 방법이다.라고 공부했습니다.
카르노 맵에서 네모칸은 1,2,4,8개로 묶었습니다.
1은 중복하여 묶어도 상관없다.
여러 가지 문제를 풀어보면서 어떤 네모를 먼저 묶어나가야 할지에 대한 고민을 했을 것입니다.
이번 포스트에서는 어떤 네모를 먼저 묶어야 하는가에 대해 알아보겠습니다.
우리가 알아야 할 내용은
PI (Prime Implicant)
PI 중에서도 더 중요한 EPI (Essential Prime Implicant)
이런 내용의 배경이 되는 I (Implicant)에 대해서도 알아봅니다.
예제로 먼저 설명하겠습니다.

입력은 WXYZ이고 출력은 F인 논리 함수가 있습니다.
카르노 맵으로 최적화해보겠습니다.

위와 그려서 다음과 같은 논리 함수 F로 최적화된다고 생각할 겁니다.
여기서 다음 문제로 넘어가면 틀리게 됩니다.
이유: 위 논리 함수에서 필요 없는 항이 있다.
? 2번 : 분홍색 네모와 빨간색 네모만 가지고도 맵에 있는 모든 1들을 커버할 수 있다. 연두색 네모는 없어도 된다.

왜 이런 실수를 했는가? 생각 없이 묶었기 때문에 , 순서를 고려하지 않고 묶었기 때문입니다.
체계적으로 묶는 방법은 뭐가 있는지 알아봅시다.
PI라는 개념에 대해서 알아보겠습니다.
PI: 각각의 1에 대해서 가장 큰 네모를 작성한다.
방금 예제에서 사용했던 K-map를 이용해서 알아보겠습니다.
m0의 위치부터 생각해봅시다.
m1을 포함하는 가장 큰 네모는?

다음과 같이 그릴 수 있습니다.

m3를 포함하는 가장 큰 네모는?
위의 그림과 같습니다.
그다음 m4에 있는 1을 포함하는 가장 큰 네모는?
두 가지 경우가 있음을 알 수 있습니다.
연두색 네모칸과 같이 그리는 경우

하늘색 네모와 같이 그리는 경우
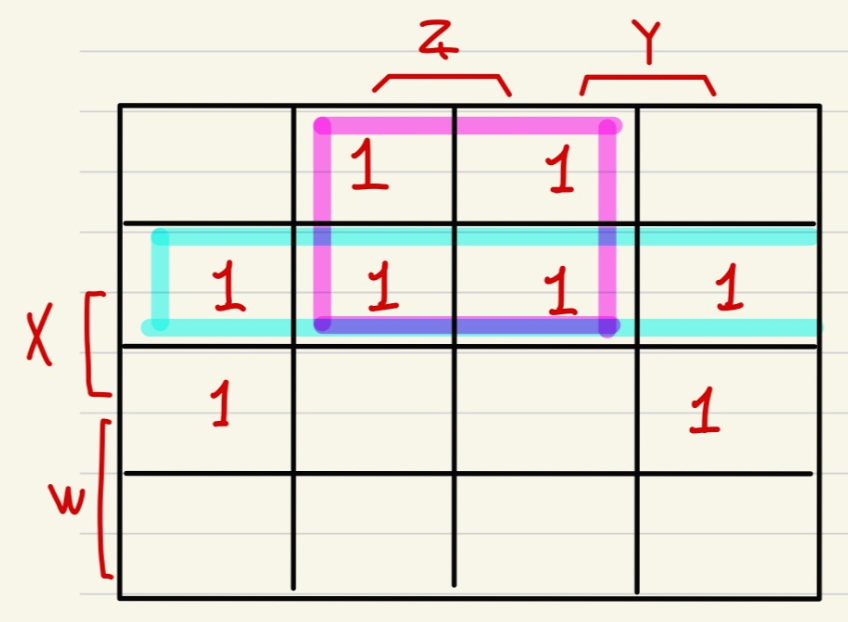
연두색 네모와 같이 그리면 PI를 찾는 과정이 끝나게 됩니다.
예제에서 주어진 논리 함수는 PI가 2개 있는 것이었다고 생각하면 됩니다.
PI의 정의가 그 1을 포함하는 가장 큰 네모를 적어둔 것이므로,.

m4까지 알아보았습니다.
모든 1이 네모칸에 다 포함되었으므로 더 이상 PI를 찾을 필요가 없습니다.
EPI에 대해서도 알아보겠습니다.
Essential : 꼭 필요한 이라는 뜻
EPI는 꼭 필요한 PI라는 뜻입니다.
EPI: PI 중에서 EPI가 되려면 어떤 기준을 만족해야 되는가?
EPI가 되려면 그 PI에만 속해있는 1이 하나 이상 있어야 합니다.
/W Z >> EPI 인지 판별해 보겠습니다.
예를 들어 분홍색 네모에서 1이 4개가 있는데 그중에서 2개는 다른 PI에 포함되어있지 않습니다.
/W Z는 m1, m4에 위치한 1 때문에 EPI가 될 수 있는 것입니다.

하늘색 네모로 만들어진 PI가 EPI인지 살펴보겠습니다.
음..... 모든 1이 다른 네모칸에 포함되어 있으므로 EPI가 아닙니다.

연두색 네모로 만들어진 PI를 살펴보겠습니다.
m12, m14에 위치한 1이 다른 PI에 포함되지 않기 때문에 /W X는 EPI임을 알 수 있습니다.

최적화된 수식을 작성할 때는 모든 EPI를 포함해서 작성하면 됩니다.
그런 뒤에 EPI로 커버되지 않는 1은 남은 PI 중에서 취사선택하여 모든 1이 네모칸 안에 둘러싸이게 하면 됩니다.
아래 문제들로 연습해보길 바랍니다.
첫 번째 문제

F대로 카르노 맵을 다시그려보면 다음과 같습니다.

위의 EPI대로 카르노맵을 그리면 아래와 같습니다.

m14에 포함되어있어야 하는 1이 없습니다.
이 1을 포함시켜주는 네모칸을 찾아서 작성해주어야 합니다.
두 가지 답이 나오게 됩니다.
검은색 네모로 묶는 경우

파란색 네모로 묶는 경우


두번째 문제(?)
2-19(a)




세번째 문제
F= XZ + /W X /Y + WXY+ W/YZ PI를 찾고 EPI를 찾고 F를 최적화하라.




EPI 4개 만작 성해도 모든 1들을 다 커버하게 됩니다.
도움이 되셨다면 로그인이 필요없는 하트버튼 한번 부탁드립니다!!
'내가 공부한 3학기 전공 > 내가 공부한 논리회로 설계' 카테고리의 다른 글
| 내가 공부한 논리회로설계 20.Other Gates (NOR,NAND) (0) | 2020.05.28 |
|---|---|
| 내가 공부한 논리회로 설계 19. POS_Don't Care (0) | 2020.05.19 |
| 내가 공부한 논리회로설계 17.k-map(4 inputs) (1) | 2020.05.11 |
| 내가 공부한 논리회로 설계16.K-map (3 inputs) (0) | 2020.05.08 |
| 내가 공부한 논리회로 설계15. K-map (2 inputs) (4) | 2020.05.06 |




