공머씨의 블로그
내가 공부한 논리회로 설계 24.(13_2.Coder_Line Decoder_Encoder) 본문
내가 공부한 논리회로 설계 24.(13_2.Coder_Line Decoder_Encoder)
공머씨 2020. 6. 11. 19:53
몇 가지 재미있는 회로에 대해 공부해봅니다.
3.4 Selection Circuits중에서 Multiplexer이라는것이 있습니다.
Line Decoder와 Multiplexe를 조금 더 비중있게 공부합니다.
Decoder에 대해 먼저 알아봅니다.

Decoder는 Encoder와 하나의 pair입니다.
(Encode:암호화 하다)
MP3,MPEG4,JPG 와 같은것들 모두 압축파일 입니다.
원래Original정보를 다른 형태로 변환해 놓은것, (통상적으로 정보량을 압축시켜놓는것이 많습니다.)
그런 변환된 신호를 만드는 과정을 "Encoder"라고 합니다.
Origine 데이터 형태로 복구하는것을 Decoder이라고 합니다.
어떤 영상을 mp4로 압축시키고 (Encoder)
영상플레이어에서 다시 mp4형태로 재생시킬 수 있습니다.(Decoder)
요약
original데이터를 다른형태로 바꾸는 과정을 Encoder이라고 합니다.
변형된형태의 데이터를 다시복원하는것을 Decoder라고 하는구나.. 정도로 알아두면 됩니다.
디지털회로에서는 Decoder의 의미가 약간 다릅니다.

Line decoder를 공부합니다.
일단 Line decoder는 n-to-m line decoder
n이 의미하는것은 input,m이 의미하는것은 output가 됩니다.
1-to-2line Decoder 라는것은 입력이 하나이고 출력이 2개인 line decoder라고 알아두면됩니다.
이렇게 읽는거구나를 알아두고, lineDecoder가 뭔지를 알아봅시다.
간단히 이야기 하면
3-to-8 line decoder 라고 하면 (입력이 3개 출력이 8개)
출력이 입력의 Minterm들일때 LineDecoder라고 합니다.
"2-to-4 line Decoder"에서는 출력4개가 입력2개의 minterm들일때
line Decoder라고 합니다.
예를 들어보겠습니다.
먼저 1 to 2 Line Decoder를 알아봅니다.
입력이름을 A라고 합니다.
입력이 하나 있고 어떤 회로를 거치면 출력이 2개 나옵니다.
출력의 이름을 D0 D1이라고 합시다.

"line decoder가 되기 위해서는 출력이 입력의 Minterm들이다." 라고 했습니다.

그래서 이 회로가lineDecoder가 되려면 출력들이 입력들의minterm이 되어야합니다.
A라고 입력변수가 하나이니까 Minterm은 2개가 있습니다 A ,/A이 있습니다.
회로를 그려본다면 다음과 같습니다.

하나는 /A이고 하나는 A 입니다.
이런 회로가 있다면 1 to 2 LD라고합니다.
입력이 N개, 출력은 2^N개 일때, 그리고 출력이 입력의 Minterm들로 구성될때 LD가 됩니다.
왜지...???
다른예시를 보겠습니다.

입력이름을 A1 A0,출력이름을 D0 D1 D2 D3 라고 붙입니다.
2-to-4 LD가 되려면 출력이 입력의 minterm들이어야 합니다.
A1 A0로 만들수 있는 minterm들은 4개가 있습니다.


A1A0에 00부터11까지 대입하면
00일때는 D0가1
01일때는 D1이1
10일때는 D2가 1
11일때는 D3가 1이 됩니다.
"LD의 출력중에 하나만 1의 값을 갖는다"라는 특징을 갖습니다.
LD의 출력은 특정순간에 하나만 1이어야 합니다. 나머지는 모두 다 0이어야 합니다.
한번 그려보면서 깔끔하게 그려보는 연습을 하는것도 좋을것 같습니다.(시험본후 수정하기)
왜 그러냐면 출력이 입력의 minterm들 이기 때문입니다. 그 중 하나만, 특정입력에 대해 1이 나오게 됩니다.
3-to-8 Line Decoder에 대해 공부해보겠습니다.
입력이 3개가 있고 출력이 8개인 3-to-8 LD의 경우입니다.
A0 A1 A2가 있고 회로의 출력이 8개가 되는 경우 입니다.

Symbol로는 다음과 같이 표현한다고 합니다.



각 출력의 논리식들은 위와 같아야 합니다.
(LD가 되려면)
직접 구현해보면 다음과 같은 형태가 나옵니다.
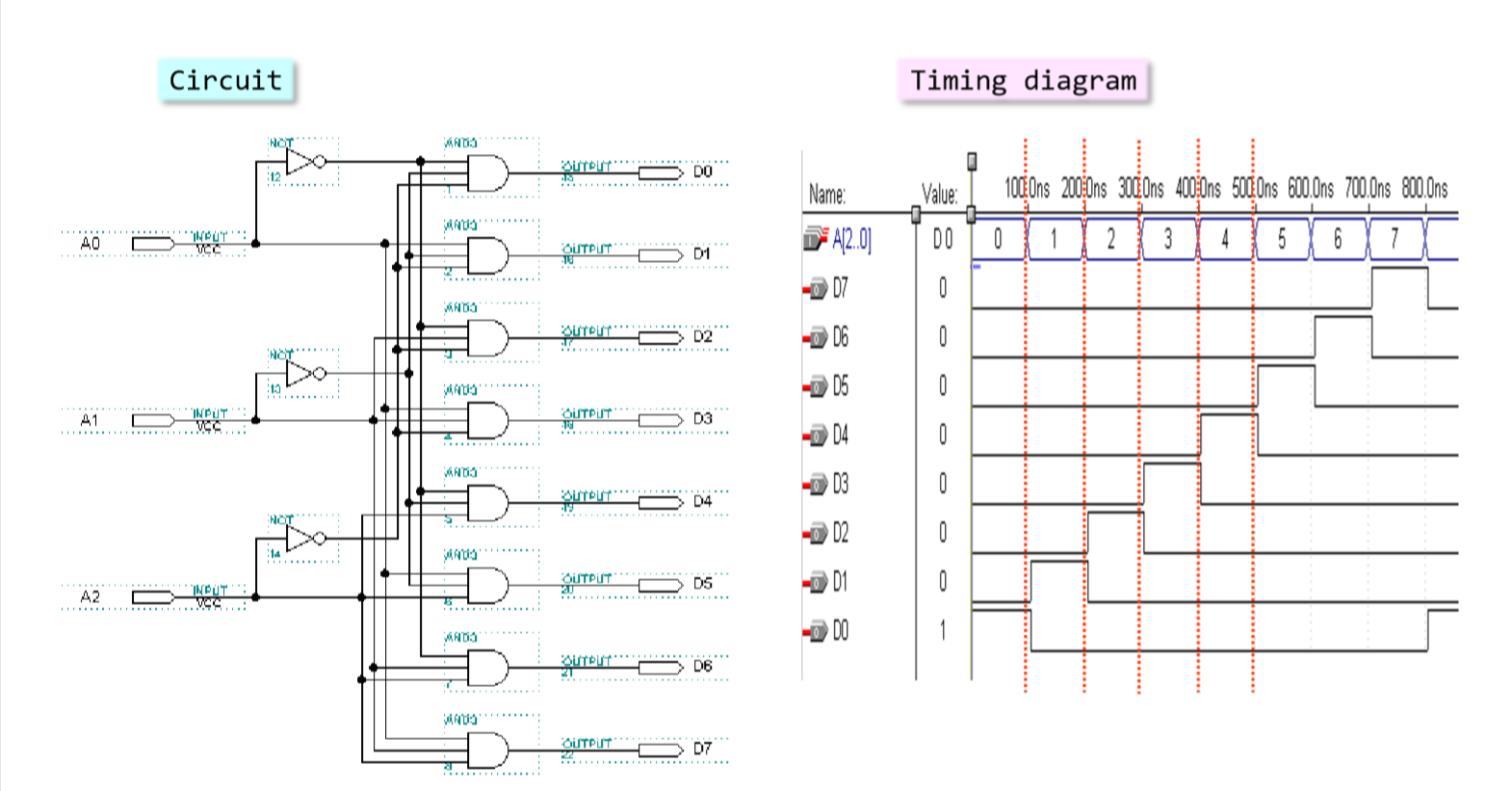
위의 방법대로 설계하면 입력이 많아 질 수록 복잡한 회로가 됩니다.
LineDecoder를 다른 형태로 설계할 수도 있습니다.
한번에 설계하는 방법도 있습니다.
예를 들어 입력이 A0 A1 A2 A3로 4개가 된다면, 16개의 출력이 필요합니다.
작은 사이즈의 LD를 병합해서 큰 사이즈의LD로 만들수 있습니다.

3-to-8 LD를 만들기 위해, 2-to-4 LD, 1-to-2 LD를 각각 하나씩 활용해서 입력이 3개이고 출력이 8개인 LD를 만들 수 도 있습니다.
노란색 형광펜으로 칠한 부분이 2-to-4 LD
연두색 형광펜으로 칠한 부분이 1-to-2 LD입니다.


입력이 4개이고 출력이 16개인 LD를 만들라는 문제입니다. 단, 2개의 2-to-4 LD와 AND게이트를 사용해야합니다.
일단 입력이 4개라는것을 먼저생각해야합니다. 출력이 16개가 있다.

두 개의 2-to-4 LD로 아래그림과같이 만들 수 있다.

그런데 우리가 원하는 출력은 A0A1A2A3이다.
아래와 같이 작성하면됩니다.
2-to-4 LD로 만든 출력들을 AND게이트로 잘 연결해주면 됩니다.

<중간 요약>
앞에있는건 입력의 개수,뒤에있는것은 출력의 개수이다.
어느하나의 출력만 1이고 나머지는 모두0이어야 한다.
출력이 입력의 Minterm들이기 때문이다. (LD의 필요조건)
큰사이즈 LD는 작은사이즈LD를 병합해서 만들 수 있다.
Enable이라는 입력을 가지고 있는 LD를 공부합니다.
Enable이라는 입력이 있다. Enable이1이면 다른 2개의 입력A1 A0의 값에 따라서 LD처럼 동작합니다.


진리표를 먼저 살펴봅니다.
Enable이 1일때 D0만 1이고 나머지는 0이다.
Enable이 1일때 A1 A0가 01 이면 D1만 1이고 나머지는 0이다.
Enable이 1일때 A1 A0가 1 1 이면 D3만 1이고 나머지는 0이다.
Enable이 1이면 A0 A1값에 의해서 D0 D1 D2 D3가 2-to-4 LD처럼 동작하고 있다.
Else
Enable이 0이라면 출력은 모두 0이다.
그런기능을 수행하면 Enable이 있는 LD라고 이야기 합니다.
진리표에서 Enable 이 0이면 A0 A1의 값에 상관없이 출력은 모두 0이 된다.
" 그런 회로가 Enable이 있는 LD이다." 라는 것입니다.
처음부터 요약
입력중에 Enable이 있습니다. 그게 0이면 출력이 모두 0이되고
Enable이 만약 1이라면 다른 입력에 따라서 LD처럼 동작을 합니다.
위와 같이 두가지 동작을 하는 회로가 됩니다.
진리표를 보면 우리가 그동안 공부했던것과 약간 다릅니다.
Condesed Truth table이라고 합니다. >> 축약된 진리표
0 X X라고 작성되어있는것은 4줄을 작성한것과 같습니다.
000 001 010 011 을 한줄로 작성한것입니다. EN이 0이면 A1 A0가 어떤 값이든 상관없기 출력이 0이 되기 때문입니다.
여기까지 이해했다면
회로를 어떻게 이렇게 구현할지를 생각해보아야 합니다.
기능을 알고 있으니까 기능대로 회로를 구현하면 됩니다.
두가지 방법이 있습니다.
1. 진리표,K-MAP으로 최적화
진리표를 봅니다.
D0 D1 D2 D3를 쭉 K-MAP으로 만듭니다.

그런데 입력이 하나 밖에 없으니 진리표를 보고 바로 Sum of minterms로 작성해도 됩니다.

2. 조건을 나타낼때는 바로 수식으로 옮겨서 작성하는 방법이 있습니다.

Enable이 1이면 그때는 LD가 동작하므로
D0=EN /A1 /A0
....
(생략)
이 부분은 뒤 에서 multiplexer를 공부할때 조금 더 상세하게 다룹니다.
지금은 EN이 있는 경우 LD의 동작에 대해 알아보았습니다.
지금 이 수식을 구현한것이 아래 회로입니다.

여기서 만약 EN이 0이었다고 한다면,A1 A0에 상관없이 값이 0이든 1이든 상관없이, 하나가 0인것입니다.
그러니까 D0 D1 D2 D3는 다른 입력에 관계없이 무조건 0이 나옵니다.
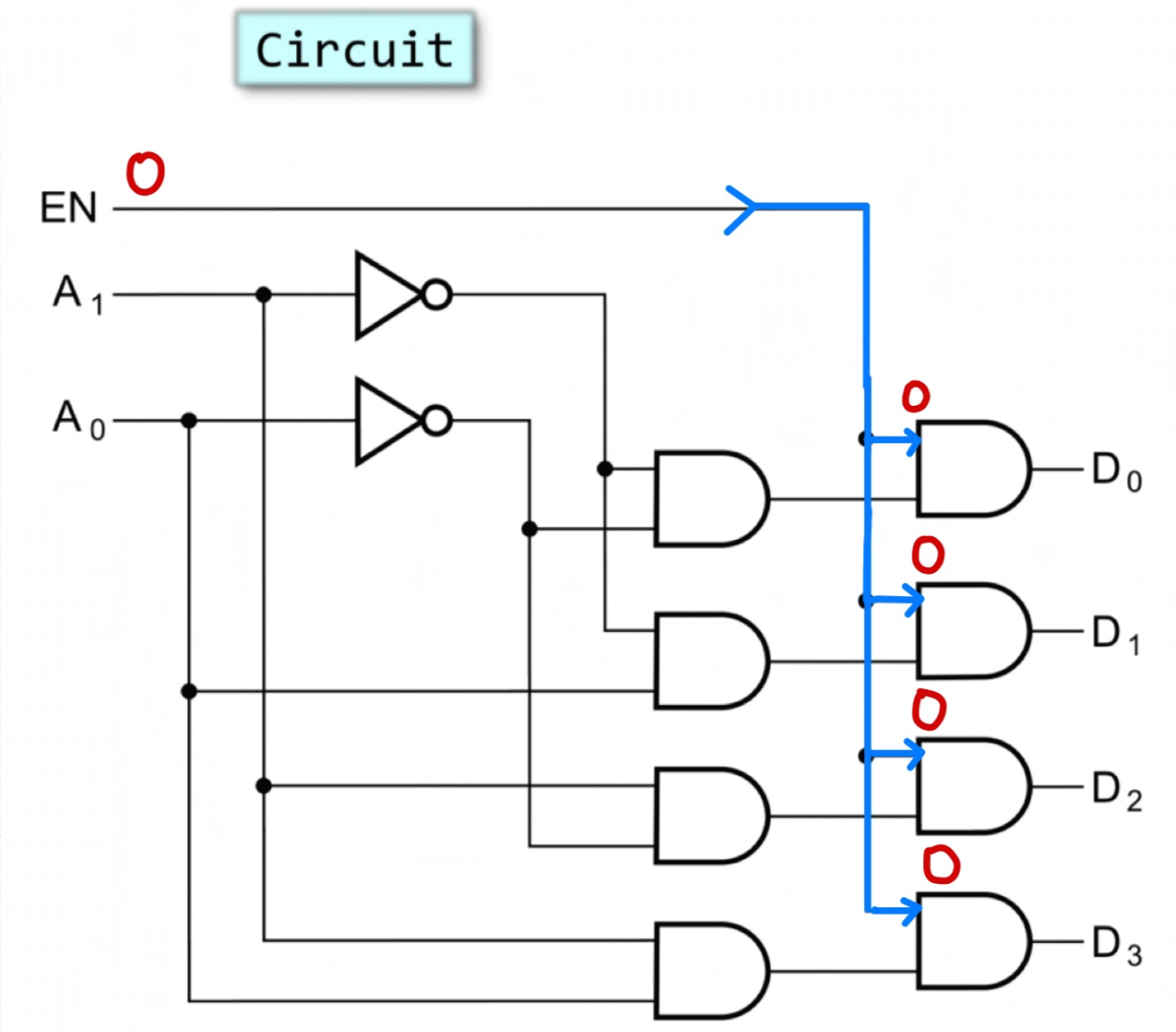
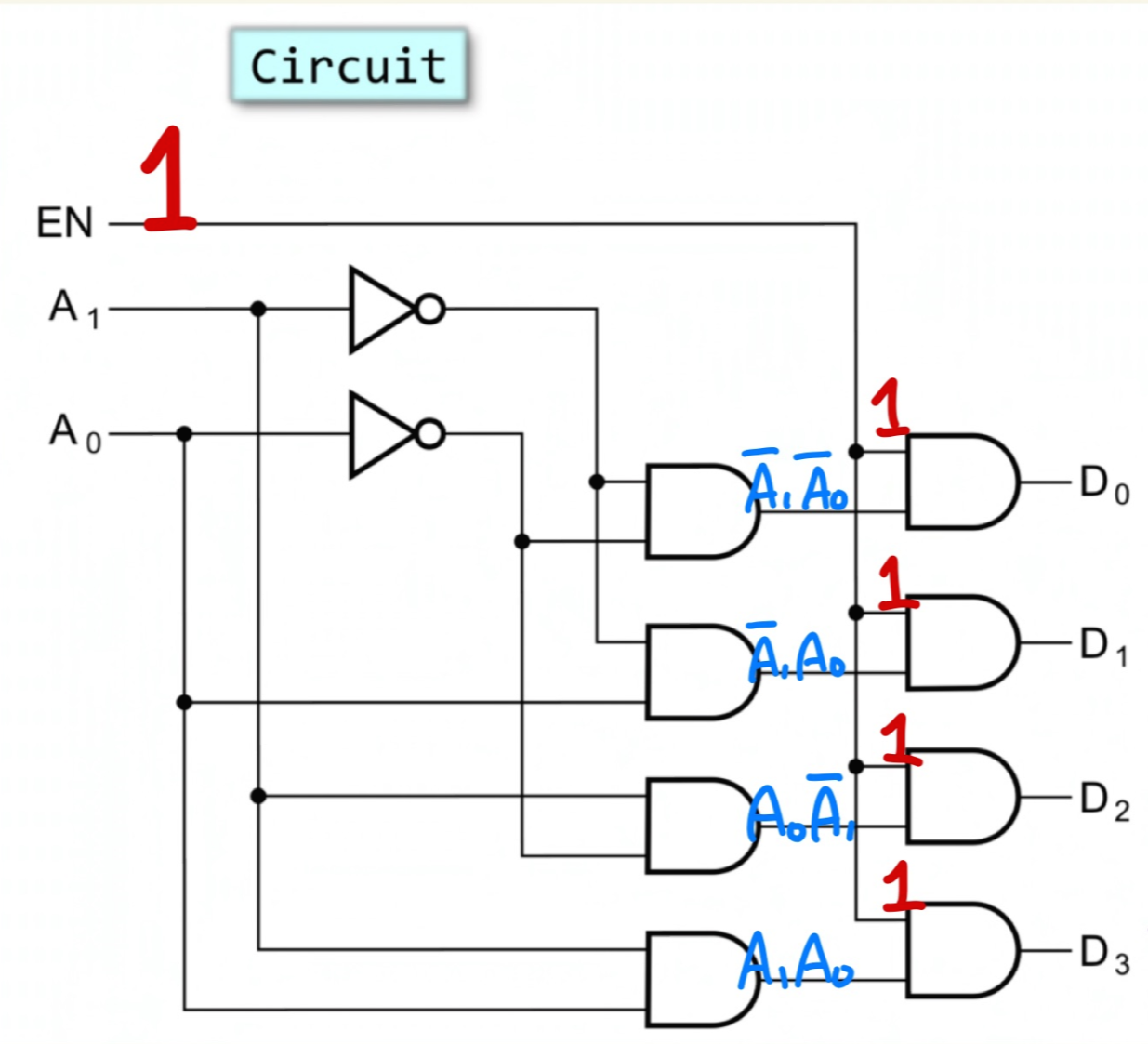
EN이 있는 LD를 여러개 활용해서 큰 사이즈 LD를 만들 수 있습니다.
다음과 같은 문제를 풀어보겠습니다.

EN이 있는 2-to-4 LD 2개와 NOT게이트 하나를 사용해서 3-to-8 LD를만들라는 문제입니다.
1.입력과 출력이 어떻게 되는지 부터
입력은 A2 A1 A0
출력은 /A2/A1/A0 /A2/A1A0 ........A2 A1 A0가 됩니다.
사용할수 있는 소자는 'EN이 있는 2-to-4 LD 2개와 NOT게이트 하나' 입니다.
EN대신에 A2가 들어왔으니까,
다음과 같이 그릴수 있습니다.

Minterm4개를 얻었으니 4개를 더 얻으면 됩니다.(총8개의 출력)
아직 사용하지않은 아래의 2-to-4 LD 를 어떻게 사용할지 생각해봅니다.
입력EN자리에 A2를 반전시켜서 넣으면 됩니다.

원하는 8개의 Minterm을 얻었습니다.


(11 12 13p인코더 부분은 생략합니다. 디코더의 입출력이 바뀐형태라고합니다.)
도움이 되셨다면 로그인이 필요없는 하트버튼 한번 부탁드립니다!!
'내가 공부한 3학기 전공 > 내가 공부한 논리회로 설계' 카테고리의 다른 글
| 내가 공부한 논리회로 설계 26(14-2)_Multiplexer (0) | 2020.06.16 |
|---|---|
| 내가 공부한 논리회로 설계 25(14-1)_Mutiplexer (2) | 2020.06.15 |
| 내가 공부한 논리회로 설계 23.(13-1_Code converter,7 segment LED) (0) | 2020.06.11 |
| 내가 공부한 논리회로 설계 22. Combinational circuit Design(Mathodology_Examples)_Majority voting circuits (0) | 2020.06.11 |
| 내가 공부한 논리회로 설계 21.XOR,XNOR게이트_Propagation delay.etc... (0) | 2020.05.31 |




