공머씨의 블로그
내가 공부한 옥타브2-들어가기전에 행렬에 대해서 본문
옥타브에서 행렬 계산을 하기 때문에 이번엔 행렬에 대해서 짚고 넘어가도록 하겠습니다.
2009 개정교육과정에서는 행렬을 배우지 않았습니다.
octave 수업에서 행렬의 덧셈 뺄셈 곱셈을 다룹니다.
물론 수업시간에 행렬의 간단한 계산을 잠깐잠깐씩 알려주시지만 바로 적용은 것은 어려울 수 있다고 생각됩니다.
이는 익숙함의 차이라고 생각합니다. 행렬이 처음이라서 계산할때 복잡해 보이고 실수도 많고 하지만 계속 찬찬히 아래의 글을 읽고 연습해보면 익숙해지면서 쉽게 느껴질 것입니다.
1. 행렬이란???
행렬(matrix)은
행과 열로 이루어져 있다.
행(row) 은 가로줄
열(column) 은 세로줄이다. 이거 햇갈리면 나중에 멘붕 온다. 첨에 잘 알아두셔야 합니다.
행렬 안에 있는숫자들을 원소(elements)라고 합니다.
가로 세로
↓ ↓
행 열
이렇게 일대일로 대응시켜서 외우면 헷갈리지 않는다.
(행열 행열 가로세로 가로세로)
아래 링크는 행렬에 대한 설명이 있는 네이버 지식백과입니다.
덧셈 뺄셈 곱셈 스칼라 배에 대하여 자세히 나와있다. 행렬의 사칙연산은 아래를 참고하는 게 좋을 것입니다.
https://terms.naver.com/entry.nhn?docId=3338358&ref=y&cid=47324&categoryId=47324
그리고 행렬의 곱셈은 헷갈리는 부분이 많기 때문에 맨아래 설명해 놓았습니다.
2. 행렬의 크기= 행렬의 차원
행렬의 크기 sizeof matrix=dimesion
행렬의 크기는 다음과 같은 행x열 의 꼴로 나타낸다.
cf) 행이 3개 , 열이 3개인 행렬의 크기는 3x3이다.
이때 행 크기와 열 크기가 같은 행렬을 정방 행렬(sqare matrix)라고 합니다.
3. 단위행렬(unit matrix)
정방행렬에서 대각선의 원소가 모두 1이고 나머지는 모두 0인 대각 행렬을 말합니다.

표기는 이렇게하고
단위행렬을 그림으로 살펴보면 아래와 같습니다.
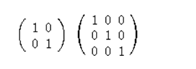
출처: 네이버 지식백과
왼쪽에 있는 행렬을 2차 단위행렬
오른쪽에 있는 행렬을 3차 단위행렬이라고 합니다.
더 나아가서 2번에서 설명한 정방 행렬은 단위행렬을 일반화한 행렬이라고 볼 수 있겠지요.
추가로
삼각함수에서 단위 원할 때 반지름이 1인 원을 단위원 이라 하고
벡터에서 크기가 1인 벡터를 단위 벡터라고 하는 것처럼
행렬에서 대각 원소가 1인 행렬을 단위행렬이라고 한다는 것을 생각하시면 됩니다.
단위행렬 I를 임의의 행렬 A와 곱하면 행렬 A가 얻어진다는 특성도 기억해 두세요
4. 대각 행렬(diagonal matrix)
대각선 원소만 0이 아닌 값을 갖고 나머지 원소는 0인 행렬.
여기서도 대각선이 기준이네요...
위 3번의 단위행렬을 일반화한 형태의 행렬이라고 생각합니다.
5. 전치 행렬(transpose matrix)
전치 행렬에서 전치는 轉 置 구를 전에 바꿀 치입니다. 치환할 때의 이와 같은 한자입니다.
A^T (A의 T승) A' 이와 같이 표기합니다.
행렬 A의 전치행렬은 A의 행 과열을 서로 바꾸어 놓은 행렬을 말합니다.
따라서
A가 2 × 3인 행렬이었다면
A의 전치 행렬의 크기는 3 × 2 가 됩니다.
그림을 통해 생김새를 확인해보겠습니다.

그림에서 보다시피 행렬 A에서의 1행은 전치 행렬에서 1열이 되었고
행렬 A에서 2행은 전치 행렬에서 2행이 되었습니다.
원소 수준에서 본다면
1행 1열 인 원소 1 은 전치 행렬에서
1열 1행으로 갔습니다.
1행 2열 인 원소 2는 전치 행렬에서
1열 2행으로 갔습니다.
원소 입장에서 보는 것보다 저렇게 행을 한 묶음 해서 통째로 옮겨준다고 생각하면 편하겠습니다.
6. 대칭 행렬(symmetric metrix)
행과 열을 바꿨을 때
바꾸기 전의 행렬 같은 행렬이 된다면
바꾸기전의 행렬을 대칭 행렬이라고 합니다.
즉
A= A^T
가 성립할 때 행렬 A를 대칭 행렬이라고 부릅니다.
대칭 행렬의 예시는 다음과 같습니다.

그림을 보고 왜 대칭 행렬인 지 생각해보면 알 수 있기 때문에 더 이상의 설명은 생략하겠습니다.
또한 나아가서 정방 행렬일 때만 대칭 행렬일 가능성이 있음을 알 수 있습니다. 이 또한 조금만 생각해보면 알 수 있기 때문에 자세한 설명은 생략하겠습니다.
7.
역행렬 (inverse matrix)이란
역행렬의 사전적 정의는 다음과 같습니다.

를 만족하는 n*n행렬 B가 존재하면 B를 행렬 A의 역행렬이라고 한다.
????? 교환 법칙이 성립한다고??????????????????
쉽게 설명해보겠습니다.
앞서 행렬에서는 교환 법칙이 성립하지 않는다고 하였습니다.
그런데
우연찮게 교환 법칙이 성립해버리는 행렬이있습니다, 또한 교환법칙이 성립해서 나온 결과가 단위행렬인 행렬이 있습니다.
이 행렬을 A라고 하고 A와 우연찮게 교환법칙이 성립되어 결과가 단위행렬이 나오게 뜸한 행렬을 B라고 합시다.
수식으로 표현하면 이렇습니다.

이때 행렬 B를 A의 역행렬이라고 합니다, 또한 이때 행렬 A를 가역 행렬(역행렬을 갖는 행렬)이라고 합니다.
표기는 다음과 같습니다.
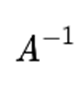
전치 행렬의 표기와 헷갈리지 않기 바랍니다.
역수를 표현할 때처럼 ‘역’이라는 글자가 들어갔기 때문에
오른쪽 위 끄트머리에 –1을 써준다고 생각하면 됩니다.
역행렬을 구하는 것에는 2가지의 방법이 있습니다.
첫 번째로는 역행렬을 구하는 공식을 이용해 구하는 방법입니다.
두 번째는 역행렬의 정의를 이용해 구하는 방법이고
역행렬 구하는 공식을 이용해 구하려면 행렬식에 대한 개념을 알아야 하는데 이는 선형대수학에서 자세히 다루도록 하겠습니다.
역행렬의 정의를 이용해서 차근차근 구해 보겠습니다.

1. 위와 같은 행렬 A 가있고 역행렬 A는 크기가 2*2라는 것만 알고 원소는 모르기 때문에 저렇게 놓습니다.
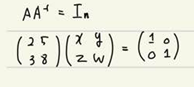
2. 위와 같은 수식을 놓고(역행렬의 정의) 방정식을 세워둡니다.

3. 행렬의 곱셈을 이용해 방정식을 풉니다.
등식 오른쪽의 결과가 단위행렬이면 됩니다.(역행렬의 정의에 따라)

4. 즉 위와 같은 방정식을 세우면 되겠습니다.
5. 그리고 계산을 하면
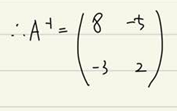
6. 위 와 같은 결과가 나오게 됩니다.
8. 행렬의 곱셈
많이 헷갈리는 연산이라서 여기서 쉽게 정리하고 넘어가 보겠습니다.
행렬의 곱셈에는 조건이 있습니다.
선형대수에서는
Conformable(적합) 해야 한다고 표현합니다.
그 조건은
AB가 가능하려면 A의 열의 수와 B의 행의 수가 같아야 합니다.
행렬의 곱셈이 어떻게 되는지 알면 왜 위조건이 성립해야만 하는지를 쉽게 알 수 있습니다.
행렬의 곱셈은 다음과 같이 합니다.
행렬 A의
1 행원 소의 1열
1행원소의 2열
1행원소의 3열을
각각
행렬 B에서
1열의 1행
1열의 2행
1열의 3행
과 곱해주면 됩니다.
1행을 1열과 곱해준다고 뭉뚱그려서 말하는데
원소 수준에서는 행렬 A의 1열을 행렬 B의 1행.... 이런 식으로 곱해준다고 봅니다.
당연히 무슨 말인지 알듯 말 듯 알 듯하면서 말 겁니다.
아래 그림으로 이해해 보겠습니다.

.
위 그림과 같이 A의 행끼리 묶어 줍니다. B 행렬은 열끼리 묶어 줍니다.
그러면 계산 할 때 헷갈리지가 않습니다.
그리고 A의 1행 2행을 1번 2번으로 표기하고
B의 1열 2열을 3번 4번으로 표기합니다.
2. 그리고 AB를 2*2로 세팅을 해둡니다
각 자리에 다음과 같이 번호를 써둡니다.
여기서 AB라는 것은 A의 행과 B의 열을 곱해준다는 것을 알 수가 있습니다.

3. 위 그림과 같이 AB행렬에서 (1행 1열 원소를 보세요)
행렬 A의 1행1열 원소를 행렬 B에서 1열의 1행과 곱 3*1
행렬 A의 1행 2열 원소를 행렬 B에서 1열의 2행과 곱 1*0
행렬 A의 1행 3열 원소를 행렬 B에서 1열의 3행과 곱 5*3
.
.
.
으로 계산됨을 알 수 있습니다.
A의 1행은 원소의 순서에 따라 B의 1열의 1행, 2행, 3행과 곱한다.
라고 말할 수 있습니다.
굉장히 복잡해 보이지만 몇 번연 습하면 익숙해지게 됩니다.
행렬에서 결합 법칙이 성립하지 않기 때문에 AB와 BA는 (B가 A의 역행렬인 특별한 경우가 아닌 이상) 같지가 않습니다.
따라서 A를 먼저 쓰냐 B를 앞 에쓰냐는 굉장히 중요합니다.
사실 행렬의 곱셈은 위의 설명을 보는 것보다 직접 몇 번 해 보고 틀리고, 해보고 틀리고, 해보고 맞고 하는 것이 더 중요합니다. 8번의 경우는 한번 읽고 계산해보고
알 것 같을 때 다시 읽어보시면 좋을 것 같다는 생각입니다.
(추가로 c언어를 하다 보면 2차원 배열이 행렬임을 알 수가 있습니다.
3차원 배열에는 면, 행, 열 이 존재한다고 합니다.)
'내가 공부한 옥타브(매틀랩) > 내가 공부한 옥타브' 카테고리의 다른 글
| 내가 공부한 옥타브5- 인터페이스 알아보기,m파일 만들기 (0) | 2020.03.11 |
|---|---|
| 내가 공부한 옥타브4-행렬입력 방법 (1~9) (0) | 2020.03.11 |
| 내가 공부한 옥타브3-인터페이스 ,내장함수(Built in function) 소개! (0) | 2020.03.11 |
| 내가 공부한 옥타브1-옥타브 소개 (0) | 2020.03.11 |
| 내가 공부한 옥타브-카테고리 소개 (2) | 2020.03.11 |



